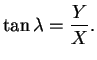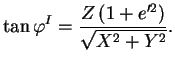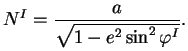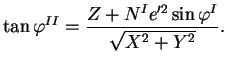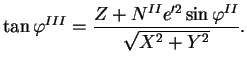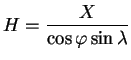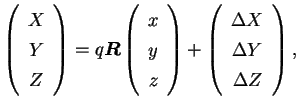Kapitola 3
Transformace mezi systémy
V této kapitole se budeme zabývat způsoby a vlastnostmi různých způsobů transformace souřadnic mezi systémy.
Uvedeme zde dva postupy, kterých bylo použito při vytváření programového modulu, a to sice postup s využitím
Helmertovy 3D transformace a převod s použitím oprav pro
 .
.
Chceme-li určit rovinné souřadnice 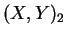 v systému 2 (např. S-JTSK), přičemž známe rovinné souřadnice
v systému 2 (např. S-JTSK), přičemž známe rovinné souřadnice 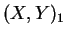 v systému 1 (např. S-42), musíme nejprve pomocí zobrazovacích rovnic získat zeměpisné souřadnice
v systému 1 (např. S-42), musíme nejprve pomocí zobrazovacích rovnic získat zeměpisné souřadnice
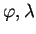 , čímž jsme se zabývali v kapitole
1. Druhým a hlavním problémem je převedení zeměpisných souřadnic z jednoho systému do druhého. Tento přepočet můžeme provést několika způsoby, a to především pomocí Helmertovy sedmiprvkové 3D transformace, nebo výpočtem diference
, čímž jsme se zabývali v kapitole
1. Druhým a hlavním problémem je převedení zeměpisných souřadnic z jednoho systému do druhého. Tento přepočet můžeme provést několika způsoby, a to především pomocí Helmertovy sedmiprvkové 3D transformace, nebo výpočtem diference
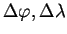 , o kterou se liší zeměpisné souřadnice
, o kterou se liší zeměpisné souřadnice
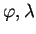 v obou systémech. Tuto diferenci můžeme vypočíst např. pomocí kubické transformační rovnice.
v obou systémech. Tuto diferenci můžeme vypočíst např. pomocí kubické transformační rovnice.
Pro použití obou metod je hlavním předpokladem znalost dostatečného počtu identických bodů, z nichž se určují transformační parametry. Přesnost transformace pak záleží hlavně na přesnosti těchto bodů a na přesnosti celé sítě, kterou je definován příslušný systém. Např. vlivem lokálních deformací v S-JTSK je pro jeho převod do WGS-84 možná přesnost transformačního klíče pro použití na celou Českou Republiku omezená.
Subsections
V případě, že chceme převést souřadnice pomocí Helmertovy 3D transformace, musíme nejprve z
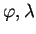 vypočítat geocentrické pravúhlé souřadnice
vypočítat geocentrické pravúhlé souřadnice 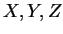 podle následujících vztahů:
podle následujících vztahů:
Elipsoidická výška H je rovna součtu jeho normální výšky 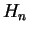 a výšky
a výšky 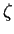 kvazigeoidu (geoidu)
kvazigeoidu (geoidu) 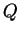 nad elipsoidem
nad elipsoidem 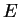 .
.
3.2 Transformace souřadnic
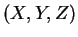 na
na
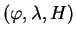
Obrázek:
Prostorové pravoúhlé souřadnice XYZ
|
Geodetickou délku 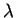 vyjádříme z prvních dvou rovnic (3.1)
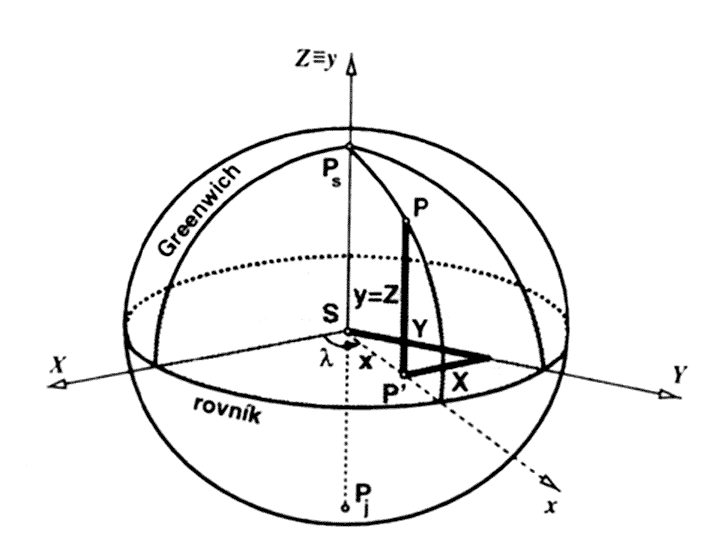
Pro geodetickou šířku
vyjádříme z prvních dvou rovnic (3.1)
Pro geodetickou šířku 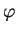 je odvození složitější a je nutné použít iteraci - viz [2].
je odvození složitější a je nutné použít iteraci - viz [2].
Výsledné iterační vzorce:
První přibližnou hodnotu geodetické šířky vypočteme ze vztahu:
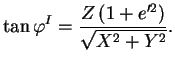 |
(3.2) |
K hodnotě
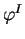 určíme odpovídající
určíme odpovídající 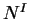 :
:
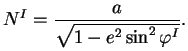 |
(3.3) |
A dosadíme do následujícího přesného vztahu, čímž určíme druhou přibližnou hodnotu
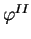 :&sstarf#star;
:&sstarf#star;
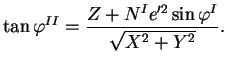 |
(3.4) |
Pro třetí aproximaci bude platit:
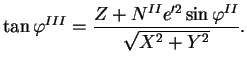 |
(3.5) |
Třetí aproximace již dává hledanou hodnotu
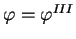 .
Ze vztahu (3.1) již snadno vypočítame výšku H:
.
Ze vztahu (3.1) již snadno vypočítame výšku H:
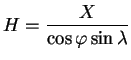 |
(3.6) |
Tento postup má následující kroky:
- Převod rovinných souřadnic
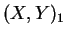 na zeměpisné
na zeměpisné
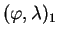 .
.
- Převod zeměpisný souřadnic
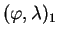 na geocentrické prostorové souřadnic
na geocentrické prostorové souřadnic
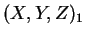 .
.
- Výpočet
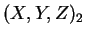 Helmertovo prostorovou transformací.
Helmertovo prostorovou transformací.
- Převod
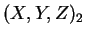 na zeměpisné
na zeměpisné
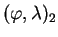 .
.
- Převod
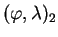 na
na 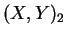 .
.
První a poslední dva kroky převodu jsou popsány v části
3.1, 3.2 a 1.1.
Souřadnice bodu vyjádříme pomocí vektoru a zavedeme následující označení:
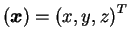 |
... |
je vektor souřadnic 1. soustavy |
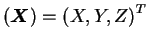 |
... |
je vektor souřadnic 2. soustavy |
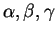 |
... |
jsou úhly rotace okolo souřadnicových os |
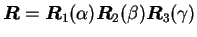 |
... |
je matice rotace |
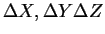 |
... |
jsou posuny ve směru os |
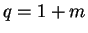 |
... |
je měřítko (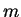 je zkreslení). je zkreslení). |
Při transformaci souřadnic v prostoru se tedy uplatní tři rotace, tři posuny a
jedno délkové zkreslení. Proto se označuje jako sedmiprvková.
Transformaci mezi soustavami můžeme zapsat rovnicí:
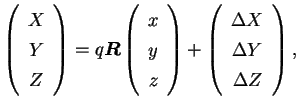 |
(3.7) |
kde matice 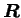 vyjádříme rovnicí:
vyjádříme rovnicí:
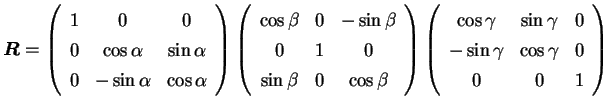 |
(3.8) |
Při aplikaci této transfomace v geodézii se setkáváme zpravidla z velmi malými
hodnotami posunů a rotací, a proto můžeme v rovnici
(3.8) goniometrické funkce linearizovat takto:
Po dosazení a roznásobení získáváme konečný tvar:
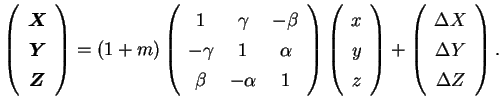 |
(3.9) |
Numerické hodnoty sedmi parametrů pro transformační rovnici většinou získáváme z
nadbytečného množství identických bodů vyrovnáním metodou nejmenších čtverců (MNČ).
Tento postup má následující kroky:
- Převod rovinných souřadnic
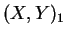 na zeměpisné
na zeměpisné
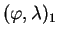 .
.
- Připočtení diferencí
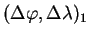 tj,
tj,
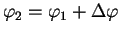 ,
,
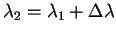 .
.
- Převod zeměpisných
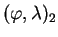 na rovinné
na rovinné 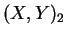 .
.
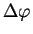 určíme pomocí kubické transformační rovnice jako funkci rovinných souřadnic
určíme pomocí kubické transformační rovnice jako funkci rovinných souřadnic 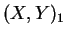 :
Koeficienty
:
Koeficienty 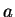 až
až 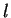 určíme z identických bodů aplikací MNČ.
Lze použít i polynom vyššího stupně, ale výsledek již nepřináší zvýšení přesnosti, nýbrž často vede k numerické nestabilitě řešení.
určíme z identických bodů aplikací MNČ.
Lze použít i polynom vyššího stupně, ale výsledek již nepřináší zvýšení přesnosti, nýbrž často vede k numerické nestabilitě řešení.
Tento postup je vhodné aplikovat pouze v území bodů, ze kterých byl určen transformační klíč. Mimo tuto oblast může získat nepřesné výsledky, jde o extrapolaci.
Jan Ježek
2003-12-17
![]() v systému 2 (např. S-JTSK), přičemž známe rovinné souřadnice
v systému 2 (např. S-JTSK), přičemž známe rovinné souřadnice ![]() v systému 1 (např. S-42), musíme nejprve pomocí zobrazovacích rovnic získat zeměpisné souřadnice
v systému 1 (např. S-42), musíme nejprve pomocí zobrazovacích rovnic získat zeměpisné souřadnice
![]() , čímž jsme se zabývali v kapitole
1. Druhým a hlavním problémem je převedení zeměpisných souřadnic z jednoho systému do druhého. Tento přepočet můžeme provést několika způsoby, a to především pomocí Helmertovy sedmiprvkové 3D transformace, nebo výpočtem diference
, čímž jsme se zabývali v kapitole
1. Druhým a hlavním problémem je převedení zeměpisných souřadnic z jednoho systému do druhého. Tento přepočet můžeme provést několika způsoby, a to především pomocí Helmertovy sedmiprvkové 3D transformace, nebo výpočtem diference
![]() , o kterou se liší zeměpisné souřadnice
, o kterou se liší zeměpisné souřadnice
![]() v obou systémech. Tuto diferenci můžeme vypočíst např. pomocí kubické transformační rovnice.
v obou systémech. Tuto diferenci můžeme vypočíst např. pomocí kubické transformační rovnice.