Křovákovo zobrazení je konformní kuželové zobrazení v obecné
poloze, které v roce 1922 navrhl Ing. Josef Křovák. Transformace
souřadnic
![]() na pravoúhlé
na pravoúhlé ![]() se provádí v
několika krocích. Nejprve je provedeno Gaussovo konformní
zobrazení Besselova elipsoidu na kouli a poté konformní zobrazení
na kuželovou plochu obecně položenou.
se provádí v
několika krocích. Nejprve je provedeno Gaussovo konformní
zobrazení Besselova elipsoidu na kouli a poté konformní zobrazení
na kuželovou plochu obecně položenou.
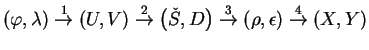
Jednotlivé kroky jsou vysvětleny v dalších paragrafech.
V první fázi je zobrazen Besselův elipsoid na kouli. Vzhledem k
tomu, že tento krok předchází zobrazení na kuželovou plochu, nazývá
se Křovákovo zobrazení dvojité. Podmínkou zobrazení je minimální délkové
zkreslení kolem základní rovnoběžky, která byla zvolena
![]() (Pro
(Pro
![]() je hodnota délkového zkreslení
je hodnota délkového zkreslení ![]() ). Pro
tuto rovnoběžku byly určeny ostatní konstanty podle
[1].
). Pro
tuto rovnoběžku byly určeny ostatní konstanty podle
[1].
Zobrazovací rovnice:
První zobrazovací rovnici i vztah inverzní lze též vyjádřit pomocí částečného součtu
řady (![]() a
a ![]() je ve stupních):
je ve stupních):
Pro délkové zkreslení platí vztah:
Křovák zvolil za zobrazovací plochu kužel v obecné poloze.
Empiricky zjistil, že ČSR lze ohraničit horizontálními kružnicemi
do pásu o šířce ![]() , přičemž zkreslení na okrajích
dosahovalo hodnot +24cm/km. V případě normální polohy kužele by
byl pás široký
, přičemž zkreslení na okrajích
dosahovalo hodnot +24cm/km. V případě normální polohy kužele by
byl pás široký ![]() a zkreslení v maximální vzdálenosti od
střední rovnoběžky až +42 cm/km. Při definitivní úpravě byla
zvolena jako základní rovnoběžka kartografická rovnoběžka
a zkreslení v maximální vzdálenosti od
střední rovnoběžky až +42 cm/km. Při definitivní úpravě byla
zvolena jako základní rovnoběžka kartografická rovnoběžka
![]() a okrajové
a okrajové
![]() a
a
![]() . Základní rovnoběžka je kolmá na
zeměpisný poledník
. Základní rovnoběžka je kolmá na
zeměpisný poledník
![]() východně od Ferra a jejich
průsečík
východně od Ferra a jejich
průsečík ![]() má šířku
má šířku
![]() . Tím je určen
kartografický pól K, který má na referenční kouli souřadnice:
. Tím je určen
kartografický pól K, který má na referenční kouli souřadnice:
Transformace
![]() :
:
Referenční koule je dále konformně zobrazena na kužel v obecné
poloze. Ve vzorcích pro kuželové zobrazení (viz
[1]) nahradíme zeměpisné souřadnice kartografickými a
získáváme tyto zobrazovací rovnice:
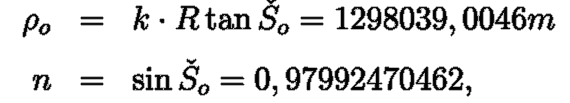
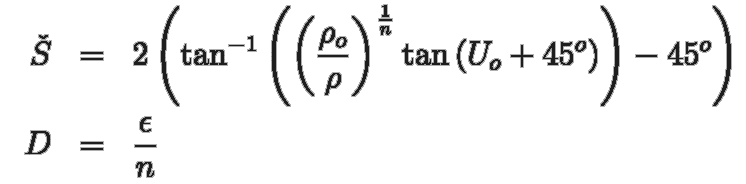
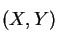
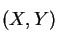 platí následující rovnice:
platí následující rovnice:
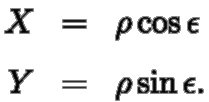
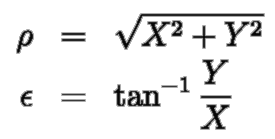
K vyjádření zobrazovacích rovnic použijeme řady:
Délku poledníkového oblouku ![]() určíme podle [2] ze vzorců:
určíme podle [2] ze vzorců:
Vztahy pro určení
![]() z daných pravoúhlých rovinných souřadnic lze určit z rovnic
(1.7) iterací - viz [1]. Výsledné rovnice:
z daných pravoúhlých rovinných souřadnic lze určit z rovnic
(1.7) iterací - viz [1]. Výsledné rovnice:
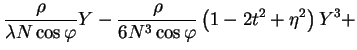 |
(1.9) | ||
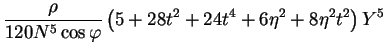 |
|||
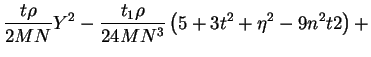 |
|||
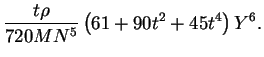 |
V rovnici pro výpočet ![]() je nutné nejprve určit
je nutné nejprve určit
![]() a z něj pak vypočítat ostatní koeficienty (
a z něj pak vypočítat ostatní koeficienty (
![]() ).
).
![]() zjistíme iterací ze vzorce (1.8), přičemž podle obr. 1.3 platí
zjistíme iterací ze vzorce (1.8), přičemž podle obr. 1.3 platí ![]() .
.
První přibližnou hodnotu
![]() vypočteme ze vzorce:
vypočteme ze vzorce:
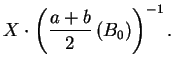 |
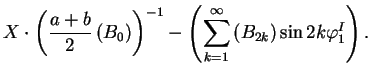 |
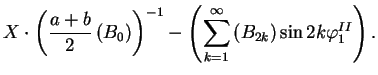 |
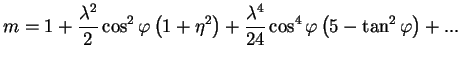
| (1.10) | |||
| (1.11) | |||
Tato úprava Gaussova zobrazení je použita v systémech S-42 a S-52, kde se zobrazují ![]() pásy Krasovského elipsoidu. V těchto systémech je volen nezkreslený osový poledník
pásy Krasovského elipsoidu. V těchto systémech je volen nezkreslený osový poledník
![]() . (Více o S-42 a S-52 v kapitole 2 .)
U mezinárodně používaného Gaussova zobrazení Universal Transversal Mercator (UTM) se délkové zkreslení na osovém poledníku
. (Více o S-42 a S-52 v kapitole 2 .)
U mezinárodně používaného Gaussova zobrazení Universal Transversal Mercator (UTM) se délkové zkreslení na osovém poledníku ![]() pásu upravuje na
pásu upravuje na
![]() , čímž je doaženo toho, že na osovém poledníku se délky zkracují (v naší zeměpisné šířce o 17cm/km) a na okrajích se o tutéž hodnotu prodlužují.
, čímž je doaženo toho, že na osovém poledníku se délky zkracují (v naší zeměpisné šířce o 17cm/km) a na okrajích se o tutéž hodnotu prodlužují.
Zobrazovací rovnice pro UTM vzniknou vynásobením pravých stran v rovnicích (1.7) modulem
![]() .
.