- Funkce pro Křovákovo zobrazení
- Funkce pro Gaussovo-Krügerovo zobrazení a zobrazení UTM:
- Funkce pro převod souřadnic mezi elipsoidy pomocí oprav
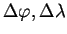
- Funkce pro Helmertovu 3D transformaci
Vzhledem k tomu, že při převodu souřadnic mezi systémy je zapotřebí provést několik kroků, byly nejprve vytvořeny funkce, které provádejí tyto dílčí kroky. Celá transformace je pak poskládána z těchto funkcí. Jelikož možností, jak převést souřadnice z jednoho systému do jiného je více, a také záleží, zda požadujeme zeměpisné, nebo rovinné souřadnice v daném systému, byl program vytvářen tak, aby mohl uživatel navržené postupy editovat, případně vytvářet částečně vlastní. Zároveň jsme se snažili o to, aby v případě potřeby doprogramování dalšího převodu byl postup co možná nejjednodušší.
Dialog programu je složen ze tří záložek. První záložka slouží k přepočtu jednotlivých bodů, druhá je určena pro transformaci celého souboru a třetí slouží k nastavení programu. Dialog programu je znázorněn na obr. ![]() .
.
sub XY_Bessel(point& P)
//XY => ro, eps
point kart,koule, kuzpol,Bessel,JTSK
JTSK=P
kuzpol.X=sqrt(JTSK.X^2+JTSK.Y^2) //ro
kuzpol.Y=atan(JTSK.Y/JTSK.X) //eps
// ro, eps => sirku, delku
real n=0.97992470462,ro0=1298039.00462
real v=tan((78.5/2+45)*PI/180), t=ro0/kuzpol.X, u=t^(1/n)
kart.X=2*(atan(v*u)-(45*PI/180)) //sirka
kart.Y=kuzpol.Y/n //delka
// sirka, delka => U,V
real Uk= 59.7118602500*PI/180
real Vk= 42.5253936806*PI/180
koule.X=asin(sin(kart.X)*sin(Uk)-cos(kart.X)*cos(Uk)*cos(kart.Y))//U
koule.Y=Vk-asin(cos(kart.X)*sin(kart.Y)/cos(koule.X)) //V
// U,V=> fi, lambda
real alfa= 1.000597498372,u0=49.4599572917,fi0=49.5
real du=(koule.X*180/PI)-u0
Bessel.X=fi0+1.001416022789*du-86.87150417/10^6*du^2+
+16.70197/10^(8)*du^3+117.5089/10^10*du^4 //fi
Bessel.Y=((koule.Y*180/PI)/alfa) //lambda
P=Bessel
end sub
Zdojový kód pro inverzní výpočet
sub Bessel_XY(point& P) point kart, koule,kuzpol,Bessel,JTSK Bessel=P // Fi, lambda => U, V real alfa= 1.000597498372,u0=49.4599572917,fi0=49.5 real dfy=Bessel.X-fi0 koule.X=(u0+dfy*(99.8585979496/(10^2))+86.50351075/(10^6)*dfy^2- -15.1091/(10^8)*dfy^3-117.3673/(10^10)*dfy^4)*PI/180 //U koule.Y=PI/180*(alfa*Bessel.Y) //V // U,V => sirka, delka real Uk= 59.7118602500*PI/180 real Vk= 42.5253936806*PI/180 //Sirka: kart.X=asin(sin(Uk)*sin(koule.X)+ +cos(Uk)*cos(koule.X)*cos(Vk-koule.Y)) //Delka: kart.Y=asin(sin(Vk-koule.Y)*cos(koule.X)/cos(kart.X)) // sirku, delku => ro, eps real n=0.97992470462,ro0=1298039.00462 //ro: kuzpol.X=ro0*((tan((39.25+45)*PI/180)/(tan(kart.X/2+45*PI/180)))^n ) kuzpol.Y=n*kart.Y //eps // ro, eps => XY JTSK.X=kuzpol.X*cos(kuzpol.Y) //X JTSK.Y=kuzpol.X*sin(kuzpol.Y) //Y P=JTSK end sub
Pro Gaussovo zobrazení jsou vytvořeny taktéž dvě funkce. První přepočítává
![]() na
na ![]() a druhá opačně. Pro tyto funkce bylo použito vzorců podle kapitoly
a druhá opačně. Pro tyto funkce bylo použito vzorců podle kapitoly ![]() :
:
sub Gauss_XY(point& P)
point S52
point Kras=P
int pas
real Ro = 57.2957795130823 ' ro ve stupnich
real LNULA, E22, E21, N, T, a, C, ETA2, LL, B,M,gama
a = 6378245: C = 6356863.019
E22 = 0.00673852541468 , E21 = 0.00669342162297
Kras.X=Kras.X/Ro, Kras.Y=Kras.Y/Ro
pas = round((Kras.Y * Ro / 6) + 1 ) // vypocet pasu
LNULA = pas * 6 - 3
LL = (Kras.Y - LNULA / Ro)
//vypocet B
B = 111134.861084 * Kras.X* Ro-16036.480269*sin(2*Kras.X)+
+16.828067*sin(4*Kras.X)-0.021975*sin(6*Kras.X)+
+0.000031*sin(8*Kras.X)
T = sin(Kras.X)/cos(Kras.X)
ETA2 = E22 * cos(Kras.X) ^ 2
N = a / sqrt(1 - E21 * sin(Kras.X) ^ 2)
//--------------------vypocet X -----------------------
S52.X=B + N * sin(Kras.X)*cos(Kras.X)*(LL^2 / 2)
S52.X=S52.X+N*sin(Kras.X)*cos(Kras.X)^3*(5-T*T+9*ETA2+
+4*ETA2^2)*(LL^4/24)
//------------------ vypocet Y -----------------
S52.Y = N*cos(Kras.X)*LL
S52.Y =S52.Y+N*cos(Kras.X)*cos(Kras.X)*cos(Kras.X)*(1-T^2+ETA2)*(LL^3/6)
S52.Y =S52.Y+N*cos(Kras.X)^5*(5-18*T^6+14*ETA2-58*ETA2*T^2)*(LL^5/120)
S52.Y =S52.Y+500000+pas*1000000
P=S52
end sub
Zdrojový kód inverzní funkce:
sub XY_Gauss(point& P) point S52, Kras S52=P int paspol real b1,b, L, M, gama real a, C, E2, EE, LNULA, LL, BR, T, N, L1, L2, L3, ETA2 real Ro = 57.2957795130823 ' ro ve stupnich //konstanty elipsoidu: a = 6378245: C = 6356863.019 E2 = 0.673852541468 / 100: EE = 0.669342162297 / 100 //vypocet pasu paspol = floor(S52.Y / 1000000) LNULA = paspol * 6 - 3 S52.Y = S52.Y - paspol * 1000000 - 500000 // iterace: b1 = S52.X / 111134.861084 BR = b1 / Ro b=b1-(-0.002518467884*Ro*sin(2*BR)+0.0000026428*Ro*sin(4*BR)- -3.681*Ro*sin(6*BR)/10^(9)) BR=b/Ro b=b1-(-0.002518467884*Ro*sin(2*BR)+0.0000026428*Ro*sin(4*BR)- -3.681*Ro*sin(6*BR)/10^(9)) BR = b / Ro T = sin(BR) / cos(BR) ETA2 = E2 * cos(BR) * cos(BR) N = a * a / (C * sqrt(ETA2 + 1)) // ------------- vypocet Lanbda ------------------- L1=(Ro*S52.Y)/(N*cos(BR)) L2=-(Ro*S52.Y^3)*(1+2*T^2+ETA2)/(6*N^3*cos(BR)) L3=(Ro*S52.Y^5)*(5+28*T^2+24*T^4+ +6*ETA2+8*T^2*ETA2)/(120*N^5*cos(BR)) Kras.Y =LNULA + L3+L2+L1 // ------------- vypocet Fi ---------------------- Kras.X=b-(Ro*T* S52.Y^2) * (1+ETA2) / (2*N^2) Kras.X=Kras.X+(Ro*T*S52.Y^4)*(5+3*T^2+ +6*ETA2-6*T^2*ETA2-3*ETA2^2-9*T^2*ETA2^2)/(24*N^4) P=Kras end subPro zobrazení UTM jsou funkce obdobné. Liší se parametry elipsoidu. Další rozdíl spočívá v tom, že hodnoty rovinných souřadnic
Tyto funkce slouží pro výpočet oprav
![]() . Opravy jsou spočítány pomocí polynomické funkce 3. stupně, přičemž vstupní souřadnice jsou rovinné souřadnice výchozího systému. Koeficienty pro polynom byly převzaty z programu Matkart.
. Opravy jsou spočítány pomocí polynomické funkce 3. stupně, přičemž vstupní souřadnice jsou rovinné souřadnice výchozího systému. Koeficienty pro polynom byly převzaty z programu Matkart.
Zdrojový kód funkce pro výpočet oprav
![]() mezi systémy S-52
mezi systémy S-52
![]() S-JTSK.
S-JTSK.
sub JTSK_S52dBdL(point& JTSK,point& D)
real kk, a, b, C, d, e, f, g, h, k, y, x , ' ro ve stupnich
y = JTSK.Y / 1000000, x = JTSK.X / 1000000
kk = -4.6646882192
a = 3.7091175824
b = -2.398277763
C = 0.33032733438
d = 0.60870873196
e = 1.0618597384
f = -0.12981050105
g = 0.011459645715
h = -0.16229009822
k = -0.011197738456
D.X = kk+a*x+b*y+C*x^2+d*x*y+e*y^2+f*x^3
D.X = D.X+g*x^2*y+h*x*y^2+k*y^3
D.X = D.X / 3600
kk = -6.799325277
a = 4.276704132
b = 10.540362944
C = -0.74948487035
d = -4.1908247218
e = 0.71106826869
f = 0.008062422824
g = 0.61432628711
h = 0.0053423421521
k = -0.20059555161
D.Y = kk+a*x+b*y+C*x^2+d*x*y+e*y^2+f*x^3
D.Y = D.Y+g*x^2*y+h*x*y^2+k*y^3
D.Y = D.Y / 3600
end sub
Jak je patrné ze zdrojového kódu, koeficinty jsou spočítané pro rovinné souřadnice vydělené 1 000 000. Výsledné opravy jsou pak určeny ve stupňových vteřinách. Funkce pro převod mezi S-JTSK
Tato funkce nejprve provede výpočet pravoúhlých prostorových souřadnic ![]() z
z
![]() podle vzorců
podle vzorců ![]() , přičemž se zanedbává výška H bodu nad geoidem, protože na výsledné rovinné souřadnice má minimální vliv. Poté je provedena transformace dle vzorců
, přičemž se zanedbává výška H bodu nad geoidem, protože na výsledné rovinné souřadnice má minimální vliv. Poté je provedena transformace dle vzorců ![]() . Nakonec jsou pravoúhlé souřadnice
. Nakonec jsou pravoúhlé souřadnice ![]() převedeny zpět na
převedeny zpět na
![]() podle postupu popsaného v části
podle postupu popsaného v části ![]() .
.
Zdojový kód funkce provádějící Helmertovu 3D transformaci:
sub Tran3D(point& P,point3D rot,point3D pos,real m,
real a,real e2,real A,real E2,real E22)
//rot se vkladaji ve vterinach
real N,W,h,Ro = 57.2957795130823,i=1
point in,out,
point3D in3D, out3D
rot.X=rot.X/3600/Ro
rot.Y=rot.Y/3600/Ro,rot.Z=rot.Z/3600/Ro
in=P
in.X=(in.X)/Ro
in.Y=(in.Y)/Ro
W=sqrt(1-e2*(sin(in.X))^2)
N=a/W
h=0
in3D.X=(N+h)*cos(in.X)*cos(in.Y)
in3D.Y=(N+h)*cos(in.X)*sin(in.Y)
in3D.Z=(N*(1-e2)+h)*sin(in.X)
out3D.X=(1+m)*( in3D.X+ rot.Z*in3D.Y- rot.Y*in3D.Z)+pos.X
out3D.Y=(1+m)*(-rot.Z*in3D.X +in3D.Y+ rot.X*in3D.Z)+pos.Y
out3D.Z=(1+m)*( rot.Y*in3D.X- rot.X*in3D.Y +in3D.Z)+pos.Z
out.Y=atan(out3D.Y/out3D.X)*Ro
out.X=atan (out3D.Z*(1+E22)/sqrt(out3D.X^2+out3D.Y^2))
W=sqrt(1-E2*(sin(out.X))^2)
N=A/W
for i=0 to 5 // iterace
out.X=atan((out3D.Z+N*E2*sin(out.X))/sqrt(out3D.X^2+out3D.Y^2))
W=sqrt(1-E2*(sin(out.X))^2)
N=A/W
i=i+1
next
out.X=out.X*Ro
P=out
end sub
Program ještě obsahuje dvě jednoduché funkce, které provádějí přepočet zeměpisné délky vztažené k Greenwichskému nultému poledníku na délku vztaženou k Ferrskému a naopak. Vztah mezi zeměpisnou délkou vztaženou k různým nultým poledníkům je:
Řídícími funkcemi programu rozumíme funkce, které realizují přenos mezi požadavkem uživatele (např. volba výchozího a cílového systému v dialogu) a správným chodem programu, tj. provedení správného algoritmu a správné výpočetní funkce.
Algoritmus celého programu je vytvořen tak, že postupy jednotlivých transformací jsou uloženy v definiční tabulce (obr.![]() ), kterou uživatel může editovat a tím si vybrat, jaký postup se bude provádět. V prvním sloupci je výchozí systém a v druhém cílový. V dalším následují jednotlivé kroky transformace, která převede souřadnice mezi systémy s využitím výpočetních funkcí popsaných v části
), kterou uživatel může editovat a tím si vybrat, jaký postup se bude provádět. V prvním sloupci je výchozí systém a v druhém cílový. V dalším následují jednotlivé kroky transformace, která převede souřadnice mezi systémy s využitím výpočetních funkcí popsaných v části ![]() . Při stisku tlačítka výpočet program prochází řádky tabulky a v případě, že v prvním políčku dané řádky najde vybraný výchozí systém (tj. systém zvolený ve výběru záložky odkud je tlačítko výpočet stisknuto), a v druhém vybraný cílový systém, provede funkce ze třetího sloupce.
Pro realizaci převodu mezi tím, jaký text se nachází ve třetím sloupci (krok transformace), a tím, jaká funkce a jakým způsobem se má použít, slouží následující funkce:
. Při stisku tlačítka výpočet program prochází řádky tabulky a v případě, že v prvním políčku dané řádky najde vybraný výchozí systém (tj. systém zvolený ve výběru záložky odkud je tlačítko výpočet stisknuto), a v druhém vybraný cílový systém, provede funkce ze třetího sloupce.
Pro realizaci převodu mezi tím, jaký text se nachází ve třetím sloupci (krok transformace), a tím, jaká funkce a jakým způsobem se má použít, slouží následující funkce:
sub vypocet(string Sysvstup, string Sysvystup, point BodVstup
point& BodVystup,string& jout,string& jin)
point D,Pom
point3D rot,pos
point P=BodVstup
real a, e2, A, E2 , E22
int i=1
int j=1
do while j<=TabCntRows(nd,nd.t)
TabGetRow(nd, nd.t, j)
if nd.t.A.Value =Sysvstup AND nd.t.B.Value = Sysvystup then
i=j
do
select case nd.t.C.Value
case "XY_Bessel"
if i=j then jin="m" //jdeli o prvni funkci vstup je v metrech
XY_Bessel(P)
jout="stup"//jednotky vystupu jsou stupne
case "Bessel_XY"
if i=j then jin="stup"
Bessel_XY(P) , jout="m"
case "Bessel_Krasovskij52"
if i=j then jin="stup"
Pom=P
Bessel_XY(Pom)
JTSKS52dBdL(Pom,D)
P.X=P.X+D.X, P.Y=P.Y+D.Y , jout="stup"
case "Krasovskij52_Bessel"
if i=j then jin="stup"
Pom=P
Bessel_XY(Pom)
JTSKS52dBdL(Pom,D)
P.X =P.X-D.X, P.Y= P.Y-D.Y , jout="stup"
case "Gauss_XY"
if i=j then jin="stup"
Gauss_XY(P), jout="m"
case "XY_Gauss"
if i=j then jin="m"
XY_Gauss(P), jout="stup"
case "Bessel_Krasovskij42"
if i=j then jin="stup"
Pom=P , jout="stup"
Bessel_XY(Pom)
JTSKS42dBdL(Pom,D)
P.X=P.X+D.X, P.Y=P.Y+D.Y
case "Krasovskij42_Bessel"
if i=j then jin="stup"
Pom=P
Bessel_XY(Pom) , jout="stup"
JTSKS42dBdL(Pom,D)
P.X =P.X-D.X, P.Y= P.Y-D.Y
case "Tran3D"
if i=j then jin="stup"
rot.X=val(nd.t.D.Value),rot.Y=val(nd.t.E.Value),rot.Z=val(nd.t.F.Value)
pos.X=val(nd.t.G.Value),pos.Y=val(nd.t.H.Value),pos.Z=val(nd.t.I.Value)
select case nd.t.K.Value
case "Bessel"
a=6377397.15508, e2=0.006674372230622
case "WGS-84"
a=6378137, e2=0.006694379990141
end select
select case nd.t.L.Value
case "WGS-84"
A=6378137, E2=0.006694379990141 ,E22=0.006739496742276
case "Bessel"
A=6377397.15508, E2=0.006674372230622
E22=0.006719218797978
end select
Tran3D(P,rot,pos,val(nd.t.J.Value),a,e2,A,E2,E22)
jout="stup"
case "Wgs84UTMBLEN"
if i=j then jin="stup"
Wgs84UTMBLEN(P), jout="m"
case "Wgs84UTMENBL"
if i=j then jin="m"
Wgs84UTMENBL(P), jout="stup"
case "Ferro_Green"
if i=j then jin="stup"
P.Y=(P.Y-(17 + 40 / 60)) , jout="stup"
case "Green_Ferro"
if i=j then jin="stup"
P.Y=(P.Y+(17 + 40 / 60)) , jout="stup"
end select
i=i+1
TabGetRow(nd, nd.t, i)
if nd.t.A.Value!="" AND nd.t.B.Value!="" then exit loop
if nd.t.C.Value=""then exit loop
loop
exit loop // po ukonceni vypoctu uz dal nehleda
end if
j=j+1
loop
BodVystup=P
end sub
Důvod, proč byl volen tento poněkud netradiční způsob volání funkcí prostřednictvím tabulky, spočívá v tom, že umožňuje velice snadno a rychle doplňovat a konfigurovat další zobrazení a převody, aniž by se musel zásadně měnit celý program. Při vytváření nové výpočetní funkce stačí jen do výše uvedené funkce vypocet zadefinovat její použití a pak ji lze jakkoliv napojovat na již vytvořené funkce prostřednictvím tabulky.
V této části stručně zhodnotíme přesnost výsledků vypočítaných vyvinutým modulem. Předmětem zájmu budou transformace mezi systémy, tedy S-JTSK
![]() WGS-84, S-JTSK
WGS-84, S-JTSK
![]() -S42 a S-JTSK
-S42 a S-JTSK
![]() S-52. Program umožňuje použít i funkce na samotné zobrazení (tj. přepočet
S-52. Program umožňuje použít i funkce na samotné zobrazení (tj. přepočet
![]() v témže systému). U těchto převodů jsou však použity přesné zobrazovací rovnice (chyba výpočtu je způsobena pouze zaokrouhlováním), takže zde se hodnocením přesnosti zabývat nebudeme.
v témže systému). U těchto převodů jsou však použity přesné zobrazovací rovnice (chyba výpočtu je způsobena pouze zaokrouhlováním), takže zde se hodnocením přesnosti zabývat nebudeme.
K otestování námi určených hodnot nezávislým výpočtem jsme použili program MATKART. V případě transformace WGS-84
![]() S-JTSK byly k dispozci souřadnice bodů DOPNUL (souřadnice jsou uvedeny v ) v obou systémech, a proto jsme provedli i porovnání s těmito přesnými hodnotami. Pro testování bylo vybráno 10 bodů rovnoměrně rozložených na území ČR podle obr. (
S-JTSK byly k dispozci souřadnice bodů DOPNUL (souřadnice jsou uvedeny v ) v obou systémech, a proto jsme provedli i porovnání s těmito přesnými hodnotami. Pro testování bylo vybráno 10 bodů rovnoměrně rozložených na území ČR podle obr. (![]() ).
).
Pro převod mezi S-JTSK
![]() WGS-84 vyvinutým modulem byla použita metoda s využitím 3D transformsce. 7 trasformačních koeficientů bylo získáno z [5], přičemž jejich hodnota byla určena pomocí bodů DOPNUL. Transformační koeficienty pro převod S-JTSK
WGS-84 vyvinutým modulem byla použita metoda s využitím 3D transformsce. 7 trasformačních koeficientů bylo získáno z [5], přičemž jejich hodnota byla určena pomocí bodů DOPNUL. Transformační koeficienty pro převod S-JTSK
![]() WGS-84 (pro opačný výpočet se koeficinty liší pouze o znaménko):
WGS-84 (pro opačný výpočet se koeficinty liší pouze o znaménko):
| Translace | |
|
|
|
|
570.8300 | 85.6689 | 462.843 |
| Rotace | |
|
|
|
|
-4.99819 | -1.58669 | -5.26130 |
| Měřítko |
|
||
![$\displaystyle m_{v}=\sqrt{\frac{[\Delta X^{2}]+[\Delta Y^{2}]}{N}}=0.230 m $](img266.png)
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pro opačný výpočet, tedy WGS-84
![]() S-JTSK, je přesnost stejná, jelikož se jedná pouze o inverzi téhož výpočtu.
S-JTSK, je přesnost stejná, jelikož se jedná pouze o inverzi téhož výpočtu.
Chyba výpočtu je způsobena tím, že S-JTSK vykazuje nepravidelně se měnící lokální deformace, a tudíž přesný transformační klíč mezi těmito dvěma systémy najít nelze.
Námi použitý klíč byl určen pro celé území z vyrovnání 175 bodů kampaně Dopnul. Platí tedy z touto přesností pro celé území. V případě, že bychom chtěli přesnější vztah, by bylo nutné zaměřit ve zkoumané lokalitě identické body a vytvořit tak přesnější klíč, který by však platil jen pro dané území. Z tohoto důvodu je funkce pro 3D transformaci naprogramována tak, aby 7 parametrů mohl nastavovat i sám uživatel.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||