Dynamický model
Záměrem úlohy je definování, zpracování a vyhodnocení modelu stárnutí objektu.
Na vybraném objektu jsme definovali konstrukční prky a jejich vzájemné interakce. Namodelovali jsme funkci stárnutí objektu jako exponenciální funkci interakcí konstrukčních prvků. Nadefinovali jsme též manažerské a externí vlivy. V poslední části modelu jsme změnili technologii provedení 3 prvků a tudíž i interakce. Nakonec jsme pro snadnější ovládání modelu nadefinovali ovládací prvky. Pro vytvoření modelu byl použit programovací jazyk VBA v EXCELu. Celý zpracovaný program naleznete ZDE.
Úloha se skládá z pěti částí :
Dynamický model stárnutí objektu (popis objektu)
Sestavení struktury modelu stárnutí objektu
Vyhodnocení změny struktury modelu
Podklady k úlohám naleznete na stránkách http://eko.fsv.cvut.cz/~dlask.
Dynamický model stárnutí objektu
Zadání:
Zpracujte model vzájemného spolupůsobení a stárnutí konstrukčních prvků stavebního objektu v čase podle uvedeného postupu. Záměrem úlohy je definování modelu, sledujícího specifika odpovídající funkcím konkrétního objektu. Očekávaným přínosem této úlohy je vytvoření a zahrnutí typických mechanismů fungujících uvnitř stavebního celku. Cílem je vytvoření vazeb a jejich modelové ověření.
Popis objektu
Modelovaným objektem je přístavba tělocvičny 1. ZŠ Rakovník. Budova se nachází ve stávající zástavbě, je připojená k původní budově základní školy a sousední budově staré pošty spojovacími krčky (viz přiložená situace).
Základové konstrukce tělocvičny i jejího zázemí jsou železobetonové. Ochrana proti zemní vlhkosti je zajištěna folií a hydroizolačním nátěrem.
Nosné stěny tělocvičny jsou železobetonové do výšky prvního nadzemního podlaží. Zbývající část nosné stěny tvoří lepené dřevěné sloupy a štítové sloupy. Obvodový plášť tělocvičny tvoří OSB desky a je vyplněn tepelnou izolací ISOVER. Jeho povrchovou úpravu tvoří laminátové desky. V úrovní druhého podlaží je fasáda prosklená otvíratelnými zdvojenými okny. Tělocvična je zastřešena vazníky z lepeného lamelového dřeva s ocelovými táhly a střešním pláštěm. Střešní plášť je zhotoven z podbití z laminátových desek, OSB desek, parozábrany, tepelné izolace, difúzní folie, další vrstvy OSB desek, živičné krytiny a stěrkové hydroizolace. Podlahu tvoří železobetonová deska se stěrkovou hydroizolací POLYCOMPAKT, na ní je pískové vyrovnávací lože a tepelná izolace a všechno zakrývají OSB desky. Konečnou vrstvu tvoří laminátová nášlapná vrstva s vysokým koeficientem obrusnosti.
První patro zázemí tělocvičny je železobetonové, druhé je vyzděno z tvárnic POROTHERM. Stropy tvoří filigránové desky a nášlapné vrstvy podlah jsou z keramické dlažby. Příčky jsou vyzděny příčkovkami POROTHERM. Vše je omítnuto vápenocementovou omítkou, jen šatny a sociální zařízení mají stěny obložené keramickým obkladem do výšky 200mm. Schody v objektu jsou železobetonové. Budova je zastřešena plochou střechou z filigránových desek, tepelné izolace a povrchové úpravy z živičných pásů a stěrkové hydroizolace.
Veškeré přípojky technického zařízení budov (vodovod, kanalizace, elektrorozvody) jsou napojeny na stávající objekt základní školy. Strojovna vzduchotechniky a kotelna jsou umístěné v suterénu zázemí tělocvičny.
Pohled 1 |
Pohled 2 |
Půdoris |
Tělocvična 1 |
Tělocvična 2 |
Konstrukční prvky objektu
Základové konstrukce
Železobetonové svislé konstrukce tělocvičny
Dřevěná nosná část tělocvičny
Obvodový plášť a zasklení
Zastřešení tělocvičny
Speciální podlaha tělocvičny
Železobetonové svislé konstrukce zázemí tělocvičny
Železobetonové vodorovné konstrukce zázemí tělocvičny
Zděné konstrukce zázemí tělocvičny
Technické vybavení
Rozpočet stavby
|
|
Cena v Kč |
|
Zemní práce |
480 880,00 |
|
Základové konstrukce |
3 733 000,00 |
|
Železobetonové svislé konstrukce tělocvičny |
657 420,00 |
|
Dřevěná nosná část tělocvičny |
843 710,00 |
|
Obvodový plášť a zasklení |
4 662 480,00 |
|
Zastřešení tělocvičny |
1 350 800,00 |
|
Speciální podlaha tělocvičny |
659 950,00 |
|
Železobetonové svislé konstrukce zázemí tělocvičny |
369 840,00 |
|
Železobetonové vodorovné konstrukce zázemí tělocvičny |
229 550,00 |
|
Zděné konstrukce a příčky zázemí tělocvičny |
562 000,00 |
|
Technické vybavení |
1 007 720,00 |
|
Dokončovací práce v zázemí tělocvičny (omítky, zateplení…) |
823 380,00 |
|
Celková cena v Kč |
15 380 630,00 |
Konstrukční prvky a prvky modelu
Konstrukční prvky Prvky modelu
Základové konstrukce Základové konstrukce
Železobetonové svislé konstrukce tělocvičny Železobetonové svislé konstrukce tělocvičny
Dřevěná nosná část tělocvičny Dřevěná nosná část tělocvičny
Obvodový plášť a zasklení Obvodový plášť a zasklení
Zastřešení tělocvičny Zastřešení tělocvičny
Speciální podlaha tělocvičny Speciální podlaha tělocvičny
Technické vybavení Technické vybavení
Vliv dopravy
Interní vlivy
Externí vlivy-zatížení sněhem
(zázemí tělocvičny není součástí modelu)
Závěr:
V této části byl popsán objekt a byly vybrány prvky modelu. Jejich vzájemný vztah je zřejmý a je důkladně popsán v další úloze.Rozhodla jsem se
Sestavení struktury modelu stárnutí objektu
Zadání:
Zpracujte ohodnocení interakcí působících mezi jednotlivými prvky navrženého modelu stavebního objektu.
Konstrukční prvky a prvky modelu
Konstrukční prvky Prvky modelu
Základové konstrukce Základové konstrukce
Železobetonové svislé konstrukce tělocvičny Železobetonové svislé konstrukce tělocvičny
Dřevěná nosná část tělocvičny Dřevěná nosná část tělocvičny
Obvodový plášť a zasklení Obvodový plášť a zasklení
Zastřešení tělocvičny Zastřešení tělocvičny
Speciální podlaha tělocvičny Speciální podlaha tělocvičny
Technické vybavení Technické vybavení
Vliv dopravy
Interní vlivy
Externí vlivy-zatížení sněhem
(zázemí tělocvičny není součástí modelu)
Úkolem úlohy je sestavení struktury modelu. Vycházíme z předpokladu, že mezi každými dvěma prvky modelu může existovat jistá interakce. Ohodnocení je vždy subjektivní, ale mělo by se opírat o skutečná měření a pozorování. Výsledky interakcí se přehledně zapíší do interakční matice. Pozici aij v takové matici je přiřazena právě zmiňované interakci mezi jednotlivými prvky modelu.
V mém modelu jsem použila dva druhy interakcí:
vyčíslení pomocí poměrové stupnice – kvantifikovaná vazba
vyčíslení pomocí absolutní stupnice – absolutní vazba
Použila jsem 3 typy interakcí. Tyto typy jsou vysvětleny níže. Všechny interakce mezi prvky naleznete ZDE.
Kvantifikovaná vazba
V kvantifikované vazbě najdeme hranice maxima, minima popřípadě optima, a přiřadíme jim hodnoty interakcí od -1 do 1. Pro naši naměřenou hodnotu se hodnota interakce vypočítá pomocí lineární interpolace.
 |
Kvantifikovaná vazba
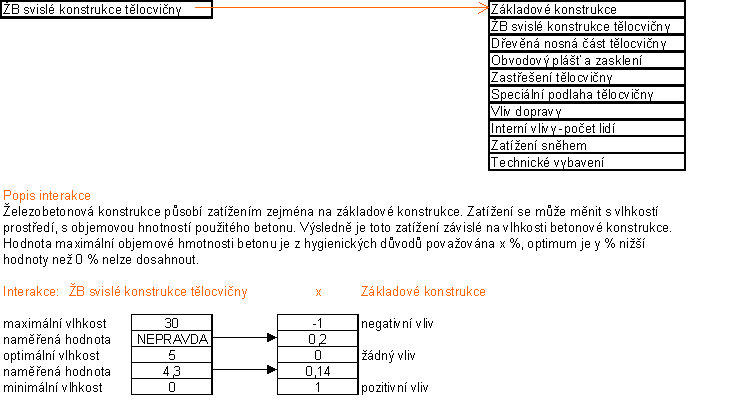 |
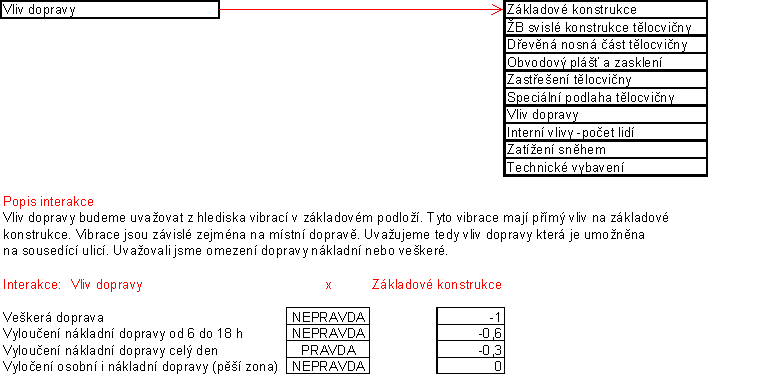
Absolutní vazba
Pro absolutní vazbu jsem si zvolila možné varianty a pro ně taky hodnoty interakcí. Pro zvolenou variantu v modelu se přiřadí hodnota interakce.
 |
Sestavená matice A
Matice A je souborem všech spočtených interakcí. Vyplňujeme ji postupně seshora, a to tím způsobem, že svislý prvek působí na prvek vodorovný.
 |
Počáteční podmínky modelu
Zvolíme si počáteční podmínky.
V případě novostavby by počáteční podmínky byly blízké nebo rovny 1. V našem případě se jedná o budovu realizovanou před dvěma lety, a proto hodnoty počátečních podmínek nebudou 1, ale budou se jim pouze blížit. Vlivy dopravy, interní vlivy a zatížení sněhem naše stavba neovlivnila, proto jejich hodnoty počátečních podmínek zůstanou rovny 1.

Sestavení výpočtu modelu
Zadání :
Zpracujte výpočet modelu pomocí procedur zapsaných v prostředí VBA tabulkového procesoru.
Pro výpočet modelu jsme použili exponenciální funkci.
Funkci jsme definovali níže uvedenými vzorci.
![]()
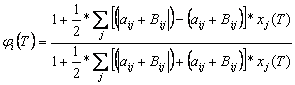
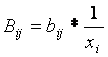
kde: Xj(T) jsou spočtené standardy v dané periodě
Xj(T+1) jsou spočtené standardy v následující periodě
aij je prvek matice A
bij je prvek matice B
Zápis procedury :
Sub vypocetmodelu()
For obdobi = 2 To (20 - 1) Step 1 Počítá přes 20 období
For i = 1 To 10 Postupně pro všechny řádky
suma1 = 0
suma2 = 0
For j = 1 To 10 Postupně po sloupcích
aij = Sheets("matice").Cells(i + 4, j + 1) Umístění matice A
bij = Sheets("matice").Cells(i + 17, j + 1) Umístění matice B
bbij = bij / Sheets("vysledky").Cells(i, obdobi - 1) Výpočet Bij
Dílčí výpočty
suma1 = suma1 + (Abs(aij + bbij) - (aij + bbij)) * Sheets("vysledky").Cells(j, obdobi - 1)
suma2 = suma2 + (Abs(aij + bbij) + (aij + bbij)) * Sheets("vysledky").Cells(j, obdobi - 1)
Next j
Výpočet a zápis výsledků
Sheets("vysledky").Cells(i, obdobi) = (Sheets("vysledky").Cells(i, obdobi - 1)) ^ ((1 + 1 / 2 * suma1) / (1 + 1 / 2 * suma2))
Sheets("vysledky diferenci").Cells(i, obdobi - 1) = Sheets("vysledky").Cells(i, obdobi) - Sheets("vysledky").Cells(i, obdobi - 1)
Next období
End Sub
Výsledky – grafy
Graf modelu
 |
Graf diferencí
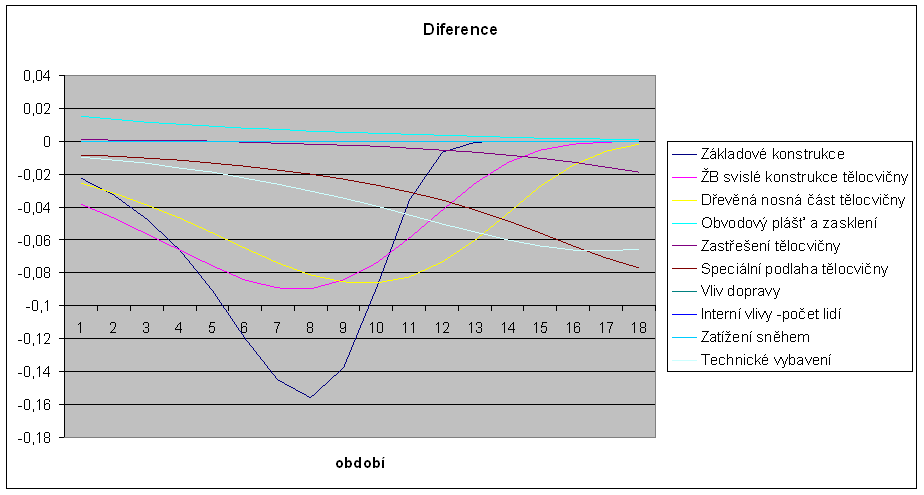 |
Regulace modelu objektu
Zadání :
Zpracujte externí regulační zásahy ovlivňující výpočet modelu objektu.
Matice B popisuje manažérské vlivy.
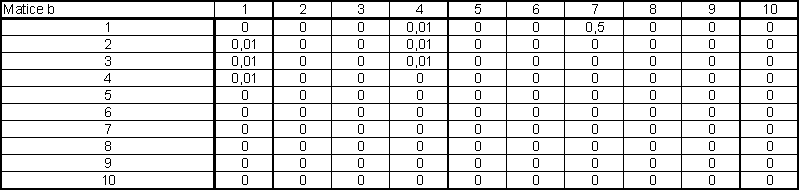
Matice externích vlivů
Matice externích vlivů popisuje zásahy do konstrukcí v různých obdobích a s jistou intenzitou. Znázorňuje velikost vlivu a jestliže působí relativně nebo absolutně.

Zápis procedury:
pro všechny i které jsou v tabulce ext. vlivů
For i = 1 To Sheets("externi vlivy").Cells(1, 3)
jestliže ext.vlivy jsou funkční (má-li se s nimi počítat), pak
If (Sheets("externi vlivy").Cells(i + 3, 6) = True) Then
jestliže ext. vlivy jsou definovány zrovna v tomto období, pak
If (Sheets("externi vlivy").Cells(i + 3, 2) <= obdobi) And (obdobi <= (Sheets("externi vlivy").Cells(i + 3, 3))) Then
jestliže jsou zásahy do ext. vlivů absolutni, pak
If (Sheets("externi vlivy").Cells(i + 3, 5) = True) Then
Sheets("vysledky").Cells(Sheets("externi vlivy").Cells(i + 3, 1), obdobi) = Sheets("externi vlivy").Cells(i + 3, 4)
jinak, neboli jsou-li zásahy do ext. vlivů relativní, pak
Else
Sheets("vysledky").Cells(Sheets("externi vlivy").Cells(i + 3, 1), obdobi) = Sheets("externi vlivy").Cells(i + 3, 4) +
Sheets("vysledky").Cells(Sheets("externi vlivy").Cells(i + 3, 1), obdobi)
End If
End If
End If
Next i
Manažerský zásah
Porovnání grafů zdůrazňuje vliv manažerských zásahů.
Rozdíly modelu
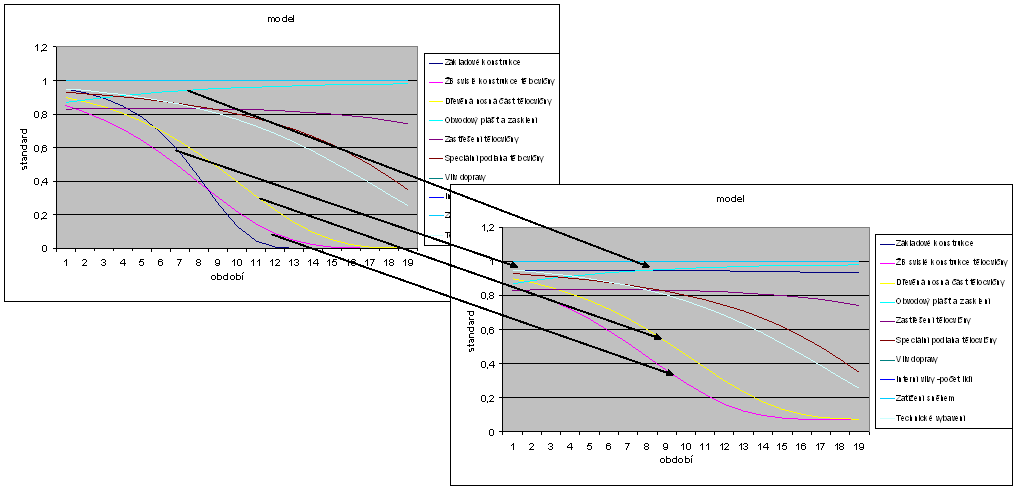
Rozdíly diferencí
 |
Externí vlivy
Porovnání grafů zdůrazňuje změnu modelu po zásahu externích vlivů.
Rozdíly modelu
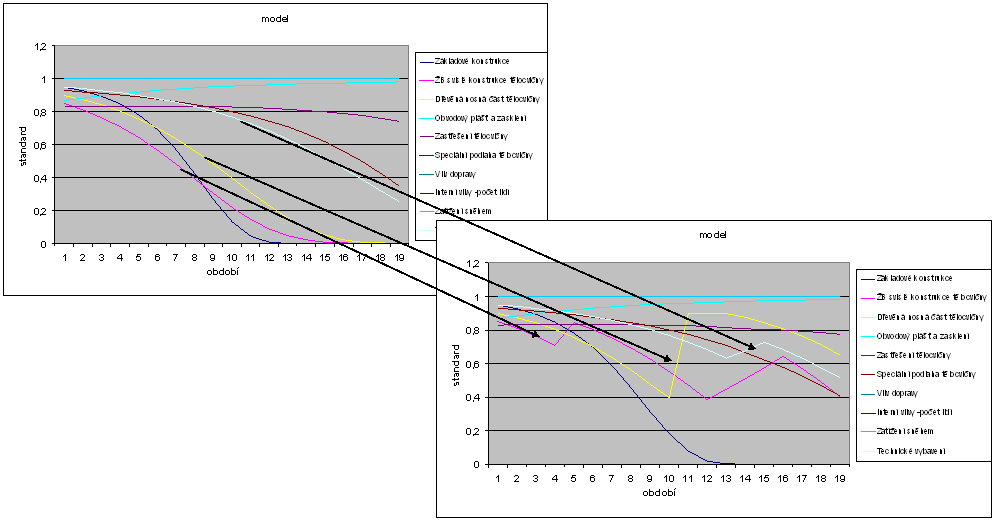 |
Rozdíly diferencí
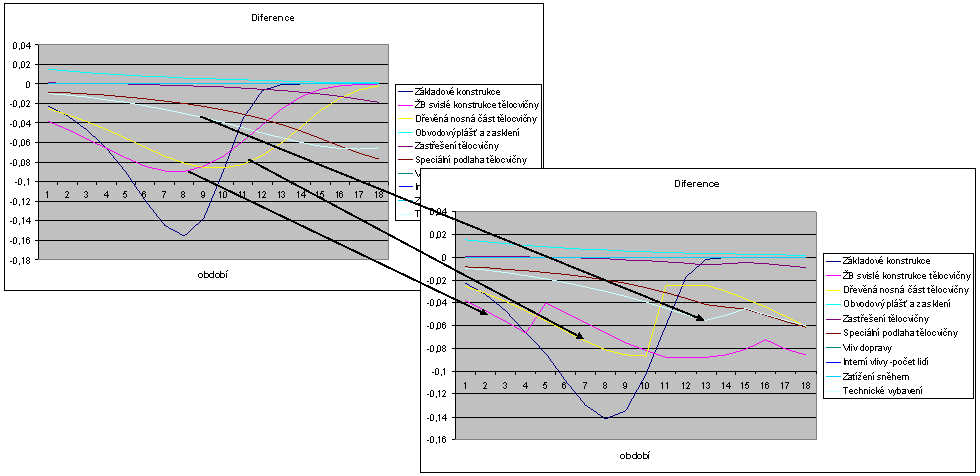 |
Vyhodnocení změny struktury modelu
Zadání :
Zpracujte modifikaci struktury matice A pro dosažení požadovaného výsledného chování modelu. Vyčíslete a zobrazte rozdíly ve fungování modelu při změně použité technologie.
Matice změn
Tuto pomocnou matici používám pro změnu technologie.
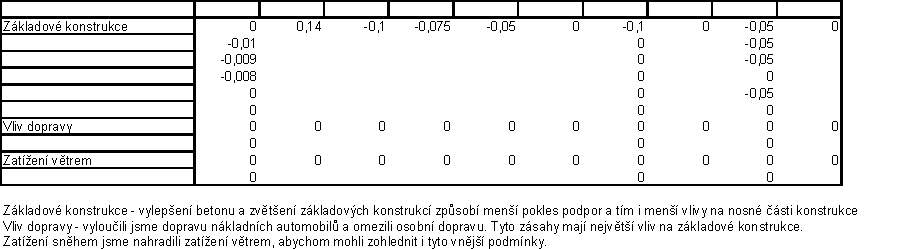
Rozdíl mezi původní maticí A a maticí po změně technologie
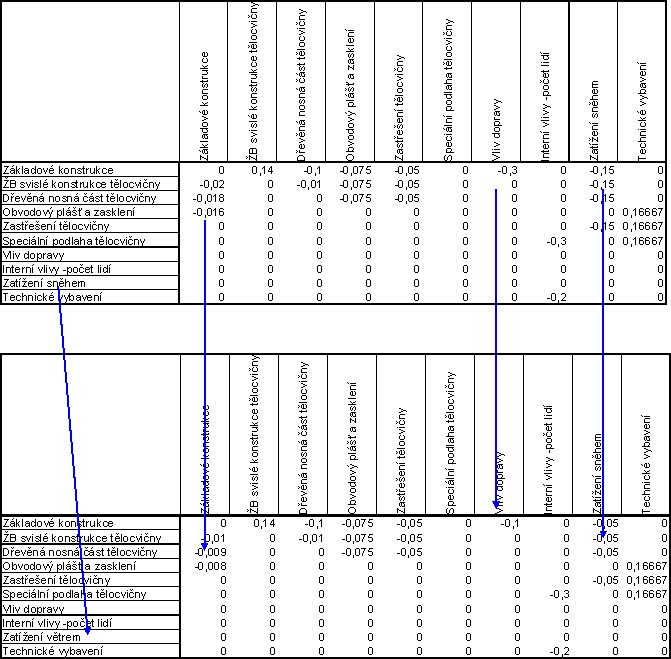 |
Grafy po změně technologie
Po změně technologie se změní skoro všechny prvky. Nejvíce je to patrné na základových konstrukcích (změna naznačena v grafu).
Rozdíly modelu
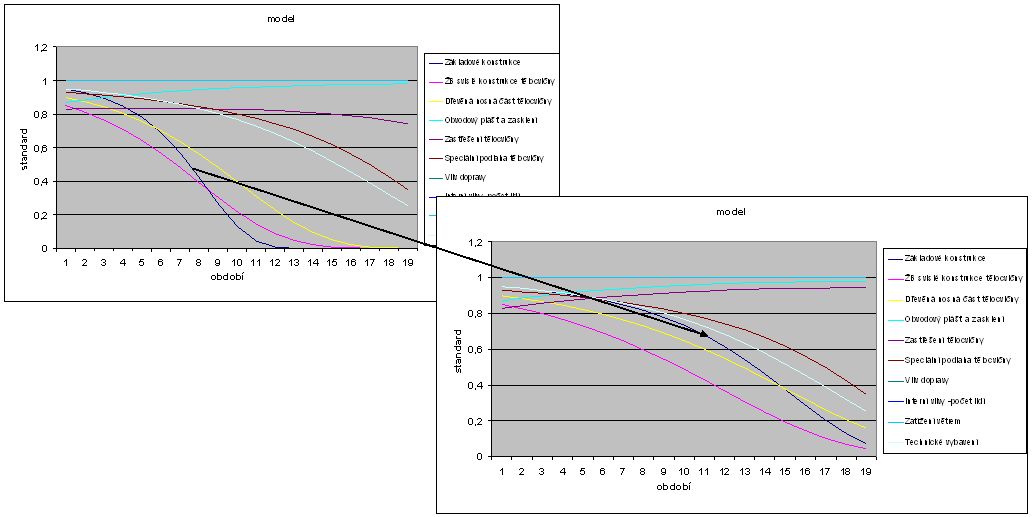 |
Rozdíly diferencí
 |
Ovládání modelu
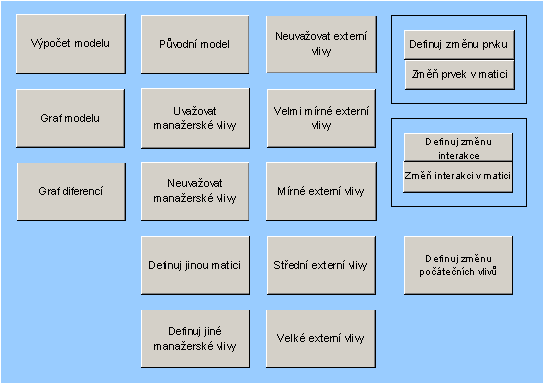 |
VÝPOČET MODELU - Vypočítá model s danými hodnotami v maticích A a B a s počátečními podmínkami , které jsou na listě "matice"
GRAF MODELU - Otevře stránku s výsledným grafem modelu
GRAF DIFERENCÍ - Otevře stránku s výsledným grafem diferencí
PŮVODNÍ MODEL - Vyplní matici A a počáteční podmínky původními hodnotami (příklad2), matici B vyplní nulovou a počet externích vlivů bude také 0
UVAŽOVAT MANAŽERSKÉ VLIVY - Vyplní matici B danými hodnotami (úloha 4)
NEUVAŽOVAT MANAŽERSKÉ VLIVY - Vyplní matici B jako nulovou
DEFINUJ JINOU MATICI -Otevře list s maticí A a je možno ručně změnit matici nebo použít matici z nějakého souboru (nakopírováním), jediná podmínka, která musí být splněna, je počet prvků (10)
DEFINUJ JINÉ MANAŽERKÉ VLIVY -Otevře list s maticí b a je možno ručně změnit matici nebo použít matici z nějakého souboru (nakopírováním), jediná podmínka, která musí být splněna, je počet prvků (10)
NEUVAŽOVAT EXTERNÍ VLIVY - Vyplní počet externích vlivů jako 0
VELMI MÍRNÉ EXTERNÍ VLIVY - Vyplní tabulku externích vlivů
MÍRNÉ EXTERNÍ VLIVY - Vyplní tabulku externích vlivů
STŘEDNÍ EXTERNÍ VLIVY - Vyplní tabulku externích vlivů
VELKÉ EXTERNÍ VLIVY - Vyplní tabulku externích vlivů
DEFINUJ ZMĚNU PRVKU - Otevře list pro změnu prvku a umožní ručně prvky změnit
ZMĚŇ PRVEK V MATICI - Změní prvky, které jsme si nadefinovali, a dosadí je do matice A
DEFINUJ ZMĚNU INTERAKCE - Otevře list interakcí a umožní je ručně změnit
ZMĚŇ INTERAKCI V MATICI - Změní interakce, které jsme si nadefinovali, a dosadí je do matice A
DEFINUJ ZMĚNU POČÁTEČNÍCH VLIVŮ - Otevře list s počátečními vlivy a je možno ručně je změnit nebo použít hodnoty z nějakého souboru (nakopírováním), jediná podmínka, která musí být splněna, je počet prvků (10)